
What You Need to Know about the CAP Theorem
The world that we live in is far from perfect. We constantly find ourselves in dilemmas, sometimes even trilemmas, that require us to make trade-offs. When shopping, we can only choose two out of “cheap,” “fast,” and “good.” In economics, a government cannot enjoy “sovereign monetary policy,” “fixed exchange rate,” and “free capital flow” at the same time. It can only achieve two of them by giving up the third. Similarly, the CAP (consistency, availability, and partition tolerance) theorem involves an equally head-scratching trilemma that has troubled computer scientists and software engineers ever since distributed computing became a popular solution to large-scale computation. Today, we will dive deep into the CAP theorem and learn how to make wise trade-offs based on our needs.
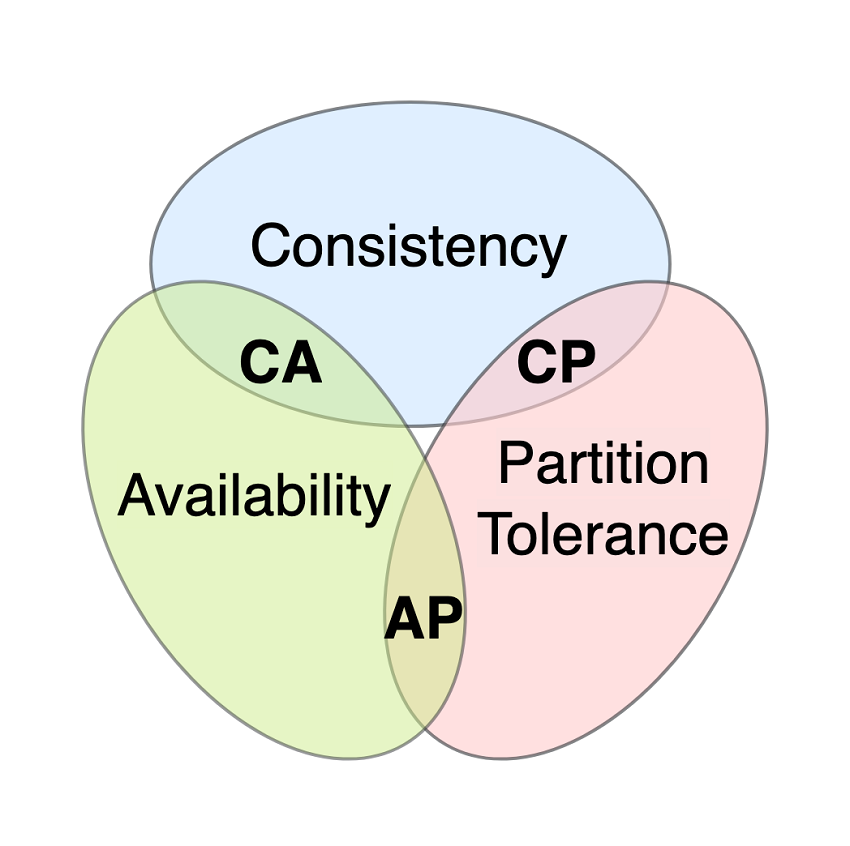
The CAP Theorem
First, let’s start with the trilemma stated in the CAP theorem. CAP stands for consistency, availability, and partition tolerance. The CAP theorem states that a distributed system can only guarantee two of these three characteristics in the face of network partitioning. Next, I will define consistency, availability, and partition tolerance in the context of the CAP theorem.
Consistency
If a distributed system is consistent, every read request receives the most recent write or an error. In other words, with consistency, no matter which node users make a read request to, they always receive the most recent data written to the distributed system or an error if the most recent data is not currently available.
Availability
Availability means that every request receives a non-error response that does not necessarily contain the most recent write. To put it another way, with availability, users always receive the data they request, but the data may be outdated.
Partition Tolerance
A distributed system that tolerates partitioning continues to operate despite an arbitrary number of messages being dropped or delayed by the network between nodes. In other words, with partition tolerance, the system remains operative even when some of its nodes cannot send messages to each other.
Some of you might ask, why can’t all three of them be achieved at the same time when network partitioning happens? While you can find a well-articulated proof of concept published by Seth Gilbert and Nancy Lynch, it might be a bit complicated and unnecessary for non-computer scientists to wrap their heads around. Therefore, I will present a shorter proof with a simple example.
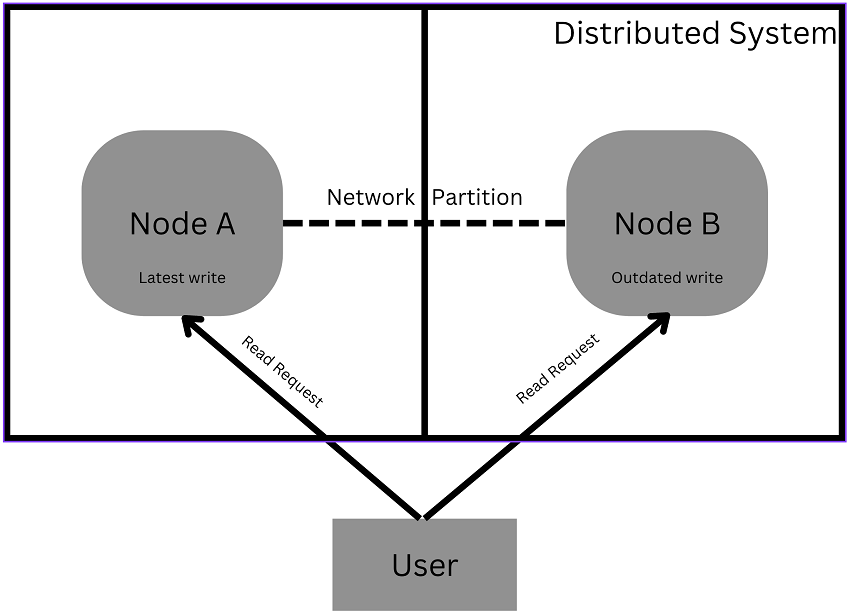
Let’s make the following assumptions: 1. We have a distributed system consisting of two independent nodes: Node A and Node B. 2. Due to network failures, these two nodes cannot receive messages from each other, i.e., the distributed system has been partitioned into two mutually incommunicable parts. 3. The most recent write is stored on Node A. 4. Since Node B cannot get messages from Node A, Node B does not contain the most recent data.
Now let’s look at why this system cannot guarantee each of these three characteristics when the other two have been achieved.
Consistency + Availability
If a distributed system is consistent and available, every read request receives a non-error response containing the most recent data when the system is running. However, we cannot achieve this because Node B cannot offer the most recent data. Therefore, to guarantee consistency and availability during the distributed system’s operation time, we have to shut it down temporarily, thus sacrificing partition tolerance.
Consistency + Partition Tolerance
With this combination, our system has to keep running and send the latest data, or an error when the latest data is unavailable, in response to read requests. Since Node B has not obtained the most recent write, it has to dispatch an error to ensure the system remains consistent. Therefore, it is impossible in this scenario to guarantee availability which requires Node B to send a non-error message.
Availability + Partition Tolerance
In this scenario, our system cannot cease operation at all times. Also, it has to respond to read requests with non-error messages. Since the most recent write is not accessible on Node B, it has no choice but to send out old data in response to read requests, consequently violating what consistency requires.
Tips on How to Choose between Consistency, Availability, and Partition Tolerance
Now that I have demonstrated it is impossible to achieve consistency, availability, and partition tolerance all at once, I will discuss how to choose between these three desirable qualities. We generally have to require our distributed systems to tolerate network partitioning for the following reasons: 1) network partitioning is ubiquitous, and 2) we want our distributed systems to remain operative even in light of network partitioning so that users won’t be confused by unhandled requests.
With partition tolerance as a must, it all comes down to a straightforward choice between consistency and availability. A rule of thumb would be to choose consistency over availability when we need to make sure users always get the most accurate data. Some good examples of systems that usually strive for consistency and partition tolerance include applications built for financial institutions such as banks and stock exchanges.
Meanwhile, we generally prefer availability to consistency when we are unwilling to forego good user experience in exchange for data accuracy. Social media platforms and games would be good examples of systems that typically aim for availability and partition tolerance.
In this article, I covered what the CAP theorem states and showed the definitions of consistency, availability, and partition tolerance. After that, I explained in detail why the trinity of consistency, availability, and partition tolerance is unachievable. In the end, I provided some tips on how to make decisions wisely in this trilemma. I hope this article has helped you gain more insight into the CAP theorem and how to apply it to your decision-making when doing system design.
In the upcoming article, I will discuss the PACELC theorem, a more comprehensive version of the CAP theorem. Please stay tuned!
